Bu bölümde kesirli sayıların bilgisayar tarafından nasıl anlaşıldığından, IEEE 754 standardından ve bazı sorunlarından bahsedeceğim.
Kayan Noktalı Sayılar
Bu bölüm daha önceki bölümden biraz daha fazla kafa karıştırıcı olabilir. İlk önce kesirli bir sayının matematiksel olarak 2 tabanına nasıl taşınacağını anlatalım. Örneğimiz 10.625 sayısı olsun. 10 sayısını 2 tabanına nasıl taşıyacağımızı daha önce anlatmıştım. Hatırlayacağınız gibi 10’u sürekli 2’ye bölüyorduk. Burda da 0.625’i 2 ile çarpacağız. Çarpımın sonucu 1’i geçerse çarpmaya virgülün sağında kalan kısmı ile devam edeceğiz. Çarpım sonucu 1.0’ı bulduğunda durmamız gerekiyor. Çarpım sonucumuzun 1’i geçtiği her işlem için 1, geçmediği her işlem için 0 veriyoruz.
0.625 x 2 = 1.25 1
0.25 x 2 = 0.50 0
0.50 x 2 = 1.0 1
En üstteki sayıyı virgülden sonraki ilk basamağa yazarak soldan sağa sayımızı yazıyoruz. Yani:
(0.625)10 = (0.101)2
10 sayısının 2 tabanında karşılığı ise 1010. Yani 10.625 sayısının matematiksel olarak 2 tabanındaki karşılığı:
1010.101
Kayan noktalı sayıları bilgisayarda işlemek için farklı yöntemler geliştirilmiş. Ben bugün güncel işlemcilerin neredeyse tamamında kullanılan IEEE 754 standardını anlatacağım. IEEE 754 standardının iki versiyonu var.
- Single precision (32 bit)
- Double precision (64 bit) Ben 32 bitlik single-precision anlatacağım. Double precision ile arasındaki farka yazının sonunda değineceğim.
İşaretli sayılarda olduğu gibi bunda da en anlamlı bit işaret biti. Pozitif için 0, negatif için 1. Arkasından gelen 8 bit exponent. Geri kalan 23 bit ise mantissa olarak adlandırılıyor.
Az önce 10.625 sayısını 2 tabanına çevirmiştik. Şimdi o örnek üzerinden devam edelim. 1010.101 sayısını bilimsel yöntemle gösterelim. Bilimsel yöntem ondalık taban için x.yzt10k. Çoğumuzun aşina olduğu bilimsel gösterime örnek: 6.02x1023. Yani bir basamak virgülün solunda kalacak şekilde yazmak. Bunun 2 tabanına çevrilmiş hali 1.xyz2t.
1010.101 sayısının bilimsel gösterimi:
1.010101*23
2’nin üssü olan 3’ü single-precisionın biası olan 127 ile toplayıp çıkan sonucu 2 tabanına çeviriyoruz.
(130)10 = (10000010)2
exponent sayımız e olsun.
bias=(2^(e-1))-1 olur.
single precision için bias=(2^(8-1))-1=127
double precision için bias=(2^(11-1))-1=1023
Çıkan sonucu 8 bitlik exponent kısmına sağa dayalı olarak, bilimsel gösterimdeki virgülden sonraki kısmıda mantissaya sola dayalı olarak yazıyoruz. İşaret bitimizi de en başa yazıyoruz. Yani:
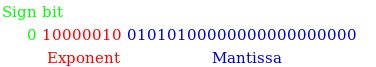
Bu sayede kayan noktalı floating-point sayılar ile işlem yapabilir, bu sayıları saklayabiliriz. Double precisionda ise 1 bit işaret biti, 11 bit exponent biti, kalan 52 bit ise mantissadır.
Yalnız bu yöntemin bazı sıkıntıları var. Nasıl 10’i 3’e böldüğümüzde 3.333…. gibi virgülden sonra sonsuza kadar devam bir sayı alıyorsak 2’yi de 3 bölersek virgülden sonra sonsuza kadar giden bir sayı alırız. Mesela 0.3 sayısını 2’lik düzene çevirmeye çalışalım.
0.3 x 2 = 0.6 0
0.6 x 2 = 1.2 1
0.2 x 2 = 0.4 0
0.4 x 2 = 0.8 0
0.8 x 2 = 1.6 1
0.6 x 2 = 1.2 1
0.2 x 2 = 0.4 0
Gördüğünüz gibi 0.01001100110011001… diye sonsuza kadar gidiyor ama bizim alabileceğimiz bit sayısı sınırlı olduğu için bir noktada kesmek zorundayız. Mesela 0.3 sayısının IEEE 754 gösterimi:
0 01111101 00110011001100110011001
Bunu tekrar ondalık tabana çevirirsek 2.9999998211860656738281250x10-1 gibi bir sayı elde ederiz. Buna benzer bir durumu terminalinizde Python yardımıyla 0.1 ile 0.2’yi toplayarak gözlemleyebilirsiniz. Daha fazla örnek için bu siteye bakabilirsiniz.

IEEE 754 standardı hakkında 2 durum kaldı. 1. durum tüm exponent bitlerinin 0 olması durumu. Bu durumda bilimsel gösterimin 1.xxxx2-127 olmasını beklersiniz. Böyle olsaydı mutlak değerce ifade edebileceğiniz en küçük sayı 110-127 olurdu. Bu yüzden tüm exponent bitlerinin 0 olduğu durumda gösterim 0.xxxx*2-126 olarak kabul edilir. Bu durumda exponent ve mantissa bitlerinin tamamı sıfır olan bir sayı 0 olur.
0 00000000 00000000000000000000000 = 0
1 00000000 00000000000000000000000 = -0
1. durum tüm exponent bitlerinin 1 olduğu durum. Bu durumda ifade sonsuz veya sayı olmaz (Not a Number, NaN).
0 11111111 00000000000000000000000 = ∞
1 11111111 00000000000000000000000 = -∞
0 11111111 xxxxxxxxxxxxxxxxxxxxxxx = NaN
1 11111111 xxxxxxxxxxxxxxxxxxxxxxx = NaN
Elimden geldiğince bildiklerimi anlatmaya çalıştım. Hatalı gördüğünüz, ekleme yapmak istediğiniz, uyarı veya öneri yapmak istediğiniz bir nokta varsa lütfen bana ulaşın.